Boundary Value Problem Using Finite Difference Method

By Vi_Gisselle556 15 Sep, 2022 Post a Comment

69 1 This Matlab script solves the one-dimensional convection 2 equation using a finite difference algorithm. The script can set either the periodic boundary conditions described in Example 1 or can set the inﬂowoutﬂow boundary condition s described in Exercise 2.

Finite Difference Method Python Numerical Methods

Y π 2 2.

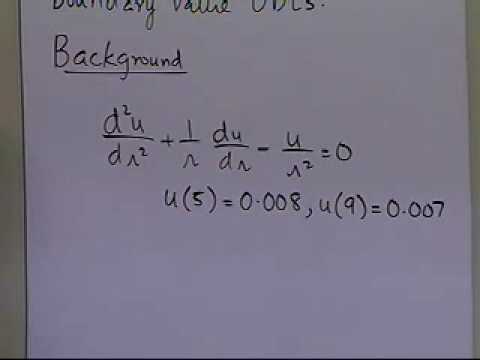
. The finite difference method is used to solve ordinary differential equations that have conditions imposed on the boundary rather than at the initial point. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Infinity norm of the Lagrangian gradient at.

16 17 Set final time 18 tfinal. So with this recurrence relation and knowing the values at time n one can. For this example use the second-order equation.

The Fast Fourier Transform is chosen as one of the 10 algorithms with the greatest influence on the development and practice of science and engineering in the 20th century in the January. Here ψ i denotes the basis functions and u i denotes the coefficients of the functions that approximate u with u hThe figure below illustrates this principle for a 1D problem. A new deterministic code ARCHER using Three-Dimensional 3-D Method of Characteristics MOC has been developed by Institute of Nuclear and new Energy Technology INET Tsinghua University aiming to obtain high-fidelity transport solution of pebble-bed High Temperature gas-cooled Reactor HTR with explicit pebble-bed geometry.

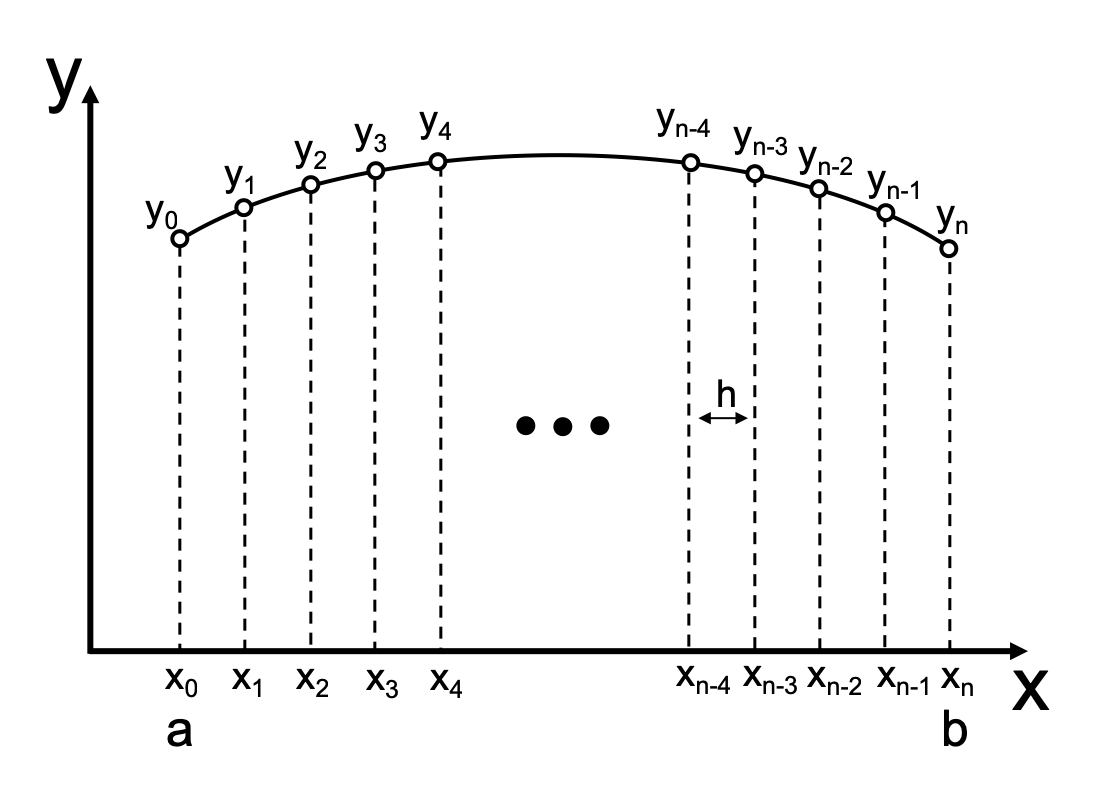
Another way to solve the ODE boundary value problems is the finite difference method where we can use finite difference formulas at evenly spaced grid points to approximate the differential equationsThis way we can transform a differential equation into a system of algebraic equations to solve. This is an explicit method for solving the one-dimensional heat equation. 1 displays the geometric settings and boundary conditions of a typical thermal cloak design problem.

The diffusion miniapp found in the miniappsshifted directory demonstrates the capability to formulate a boundary value problem using a surrogate computational domain. It means for example that if a Jacobian is estimated by finite differences then the number of Jacobian evaluations will be zero and the number of function evaluations will be incremented by all calls during the finite difference estimation. Y y 0.

The Fourier method has many applications in engineering and science such as signal processing partial differential equations image processing and so on. In mathematics in the field of differential equations a boundary value problem is a differential equation together with a set of additional constraints called the boundary conditions. 1 This Matlab script solves the one-dimensional convection 2 equation using a finite difference algorithm.

Where. In this chapter we solve second-order ordinary differential equations of the form. F x y y a x b dx d y 2 2 1.

X ndarray shape n Solution found. The rectangular domain Ω is divided into three subdomains namely the outer domain Ω out where the objective is evaluated the cloak domain or equivalently the design domain Ω c and the inner domain Ω in where the cloaking object is located. The temperature at the left and.

To solve this equation in MATLAB you need to write a function that represents the equation as a system of first-order equations a function for the. The 3 discretization uses central differences in space and forward 4 Euler in time. 5 6 clear all.

These problems are called boundary-value problems. Solve a second-order BVP in MATLAB using functions. Using a forward difference at time and a second-order central difference for the space derivative at position we get the recurrence equation.

8 9 Number of points 10 Nx 50. Y 0 0. We will look at the eigenvalues of both cases.

The equation is defined on the interval 0 π 2 subject to the boundary conditions. Boundary value problems arise in several branches of physics as any. Here the linear basis functions have a value of 1 at their respective nodes and 0 at.

11 x linspace01Nx1. . The method uses a distance function to the true boundary to enforce Dirichlet boundary conditions on the non-aligned mesh faces therefore shifting the location where.

13 14 velocity 15 u 1. U could for instance represent the temperature along the length x of a rod that is nonuniformly heated. 12 dx 1Nx.

We can obtain from the other values this way.

Finite Difference Method Initial Value Problem Mathematics Stack Exchange